Total de visitas: 51979
MMC de números Naturais
MMC - MÍNIMO MÚLTIPLO COMUM

O mínimo múltiplo comum - mmc - de dois ou mais números naturais é o menor (mínimo) número não-nulo (ou seja, diferente de zero) que seja múltiplo de todos eles (basicamente deve ser um número que esteja na tabuada de ambos os números).
Para calcular o mínimo múltiplo comum, decompomos os números em fatores primos e escolhemos os fatores comuns e não comuns, com os maiores de seus expoentes. O mmc é o produto dos fatores decompostos.
Se um número é divisível por outro, diferente de zero, então dizemos que ele é múltiplo desse outro.
Dois ou mais números sempre têm múltiplos comuns a eles.
Vamos achar os múltiplos comuns de 4 e 6:
Múltiplos de 6: 0, 6, 12, 18, 24, 30,...
Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,...
Múltiplos comuns de 4 e 6: 0, 12, 24,...
Dentre estes múltiplos, diferentes de zero, 12 é o menor deles. Chamamos o 12 de mínimo múltiplo comum de 4 e 6. Desse modo mmc(4, 6) = 12.
- CÁLCULO DO M.M.C.
Podemos calcular o m.m.c. de dois ou mais números utilizando a fatoração. Acompanhe o cálculo do m.m.c. de 12 e 30:
1º) decompomos os números em fatores primos
2º) o m.m.c. é o produto dos fatores primos comuns e não-comuns:
12 = 2 x 2 x 3
30 = 2 x 3 x 5
m.m.c (12,30) = 2 x 2 x 3 x 5
Escrevendo a fatoração dos números na forma de potência, temos:
12 = 22 x 3
30 = 2 x 3 x 5
m.m.c (12,30) = 22 x 3 x 5
|
O m.m.c. de dois ou mais números, quando fatorados, é o produto dos fatores |
- PROCESSO DA DECOMPOSIÇÃO SIMULTÂNEA
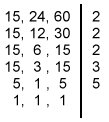
| Neste processo decompomos todos os números ao mesmo tempo, num dispositivo como mostra a figura ao lado. O produto dos fatores primos que obtemos nessa decomposição é o m.m.c. desses números. Ao lado vemos o cálculo do m.m.c.(15,24,60)
Portanto, m.m.c.(15, 24, 60) = 2 x 2 x 2 x 3 x 5 = 120 |
|